Postdoctoral research: Beyond Wild Chaos
Applied Mathematics Unit, The University of Auckland
April 2014 - present
The geometry of blenders in a three-dimensional Hénon-like family
with Bernd Krauskopf, Hinke Osinga and Katsutoshi Shinohara
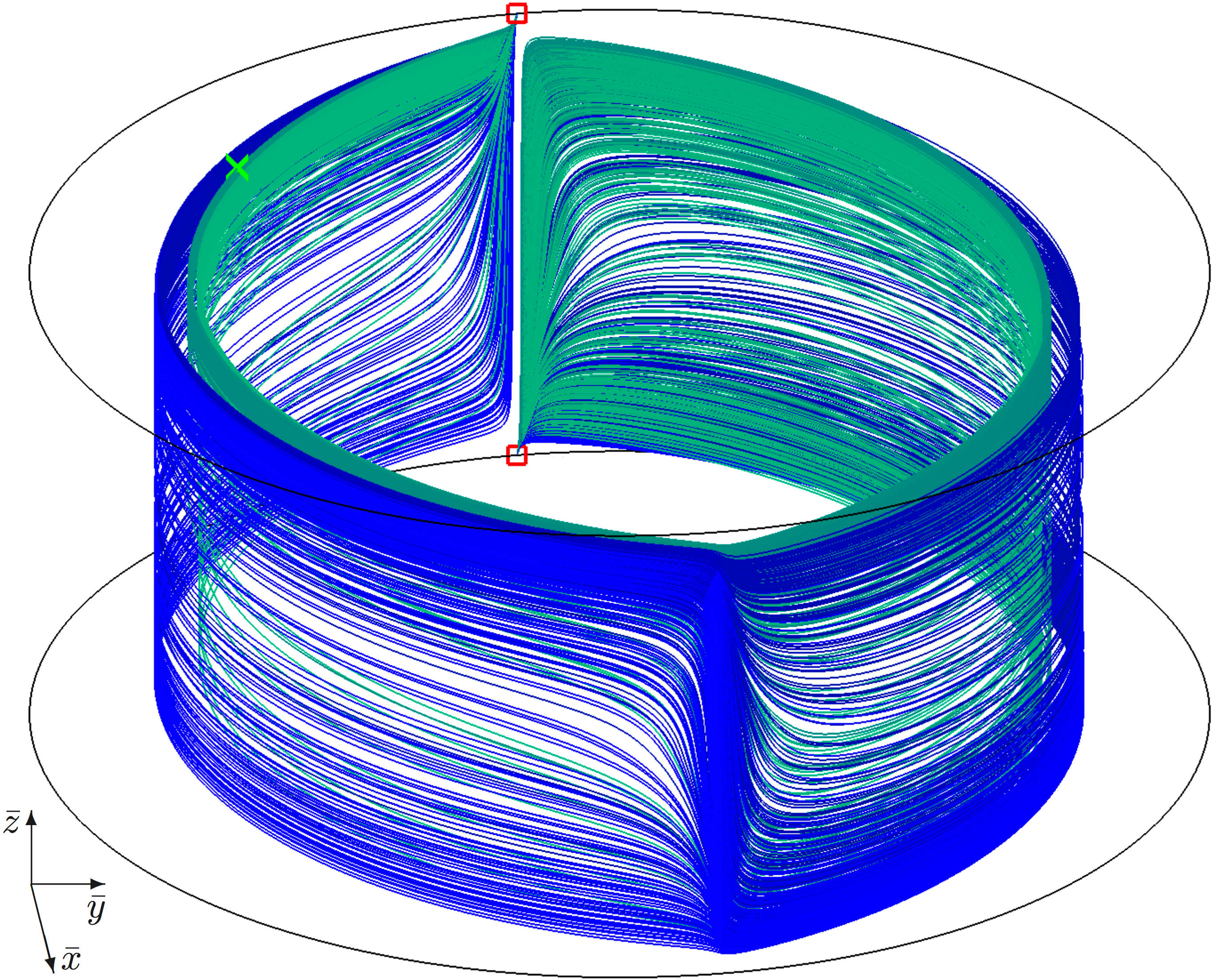A blender is an intricate geometric structure of a diffeomorphism of dimension at least three. Its characterising feature is that its invariant manifolds behave as geometric objects of a dimension that is larger than expected from the dimensions of the manifolds themselves. We consider an explicit Hénon-like family of three-dimensional maps and show that it has a blender in a specific parameter regime. Advanced numerical techniques for the computation of one-dimensional stable and unstable manifolds enable us to present images of actual blenders and their associated manifolds. Moreover, these techniques allow us to present strong numerical evidence for the existence of the blender over a larger parameter range, as well as its disappearance beyond this range.
Generalised Mandelbrot sets in a nonanalytic perturbation of the complex quadratic family
with Bernd Krauskopf and Hinke Osinga
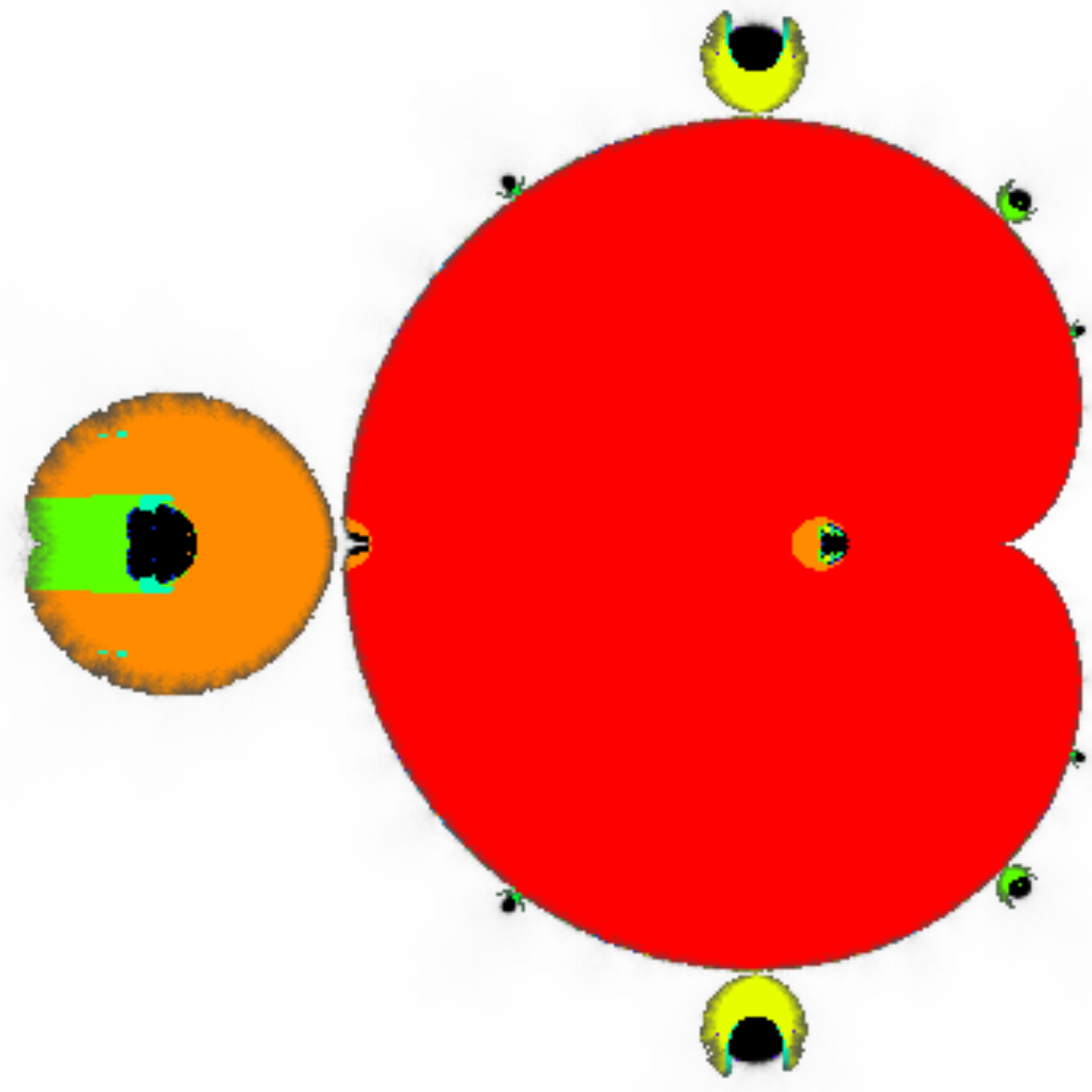
We study a planar noninvertible map that acts as a nonanalytic perturbation of the complex quadratic family. It maintains the property of angle-doubling but the critical value becomes a critical circle. As the perturbation increases the radius of the circle increases and saddle fixed and periodic points appear with their stable and unstable sets. These invariant sets interact with the critical set, given by the preimages of the critical point and the images of the critical circle, and with (generalised) Julia sets. This leads to new types of Julia sets, which is associated with the behaviour of points on the critical circle under iteration. In parameter space this is encoded by the (generalised) Mandelbrot set, which has a fat boundary. We discuss the Mandelbrot set of the perturbed map and present transitions of the Julia sets through the fat boundary.
From wild Lorenz-like to wild Rovella-like dynamics
with Bernd Krauskopf and Hinke Osinga
We consider a two-dimensional noninvertible map that was introduced by Bamón, Kiwi, and Rivera-Letelier [arXiv 0508045, 2006] as a model of a wild Lorenz-like attractor in a vector field of dimension at least five; such an attractor contains an expanding equilibrium and a hyperbolic set with robust homoclinic tangencies. Advanced numerical techniques enable us to study how the stable, unstable and critical sets of the map change within the conjectured region of wild chaos in the transition from Lorenz-like to Rovella-like dynamics, that is, when the equilibrium becomes contracting. We find numerical evidence for the existence of wild Rovella-like attractors, wild Rovella-like saddles and regions of multistability, where a Rovella-like attractor coexists with two fixed-point attractors. We identify bifurcations generating these different types of dynamics and compute them in two-parameter bifurcation diagrams.
PhD thesis: Non-invertible Maps and Wild Chaos
Applied Mathematics Unit, The University of Auckland
Supervisors: Prof. Hinke Osinga and Prof. Bernd Krauskopf
March 2010 - December 2013
We study a two-dimensional noninvertible map that has been introduced by Bamón, Kiwi, and Rivera-Letelier [arXiv 0508045, 2006] to prove the existence of wild chaos in a five-dimensional Lorenz-like vector field. Wild chaos is a type of chaotic dynamics that can arise in a continuous-time dynamical system of dimension at least four. We are interested in the possible sequence of bifurcations that generate this type of chaos in dynamical systems.
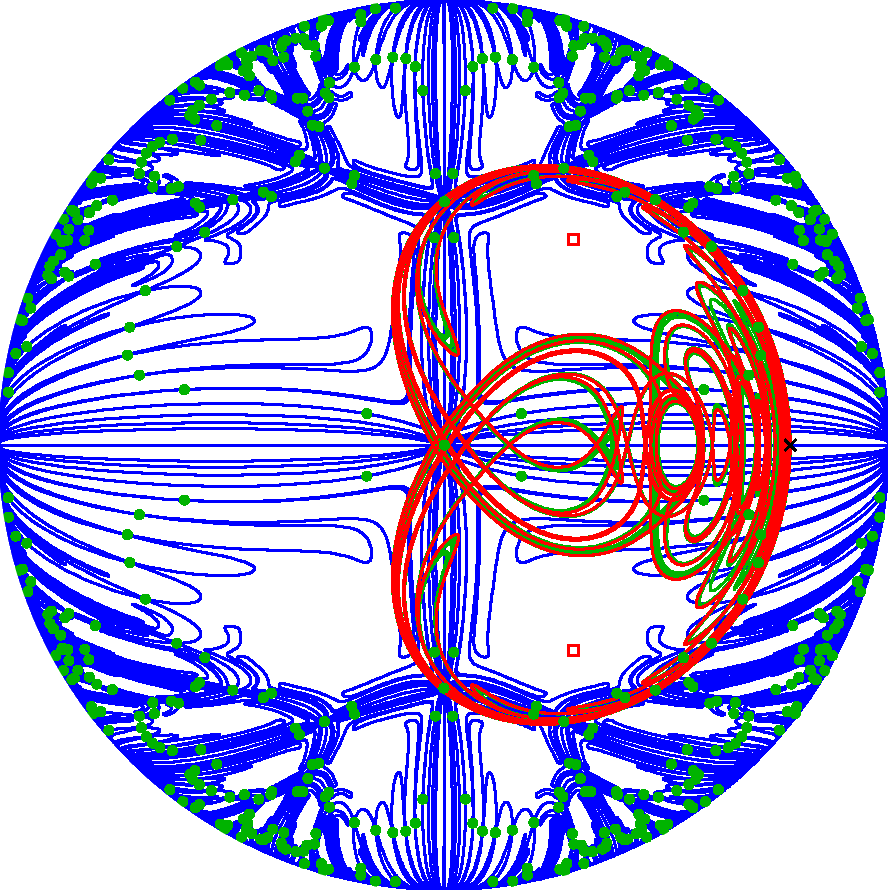The map acts on the plane by opening up the critical point to a disk and wrapping the plane twice around it; points inside the disk have no preimage. The bounding critical circle and its images, together with the critical point and its preimages, form the so-called critical set (green). This set interacts with the stable set (blue) and the unstable set (red) of a saddle fixed point and other saddle invariant sets. Advanced numerical techniques enable us to study how these invariant sets change as the parameters are varied towards the wild chaotic regime. We find four types of bifurcations: the stable and unstable sets interact with each other in homoclinic tangencies (which also occur in invertible maps), and they interact with the critical set in three types of tangency bifurcations specific to this type of noninvertible map; all tangency bifurcations cause changes to the topology of these global invariant sets. Overall, a consistent sequence of all four bifurcations emerges, which we present as a first attempt towards explaining the geometric nature of wild chaos. Using two-parameter bifurcation diagrams, we show that essentially the same sequences of bifurcations occur along different paths towards the wild chaotic regime, and we use this information to obtain an indication of the size of the parameter region where wild chaos is conjectured to exists.
In a different parameter regime, the map acts as a perturbation of the complex quadratic family and admits (a generalised notion of) the so-called Julia set as an additional invariant set. When parameters are varied, this set interacts with the other invariant sets, leading to the (dis)appearance of saddle points and chaotic attractors and to dramatic changes in the topology of the Julia set. We reveal a self-similar bifurcation structure near the period-doubling route to chaos in the complex quadratic family.
Diploma thesis: Continuation of Periodic Orbits in Conservative and Hamiltonian Systems
Research Group Numerical Analysis of Dynamical Systems, Bielefeld University
Supervisor: Prof. Wolf-Jürgen Beyn
December 2008 - November 2009
In my Diploma thesis I studied the continuation of periodic orbits in conservative and Hamiltonian systems on the basis of Muñoz-Almaraz et al. Conservative systems are dynamical systems in which certain quantaties, e.g. the total energy or the momentum, are conserved along every solution. Hamiltonian systems are conservative systems where the conserved quantities yield certain symmetries of the system. These types of systems often appear in classical and quantum mechanics.
Using the conserved quantities in conservative systems and the symmetries in Hamiltonian systems it is possible to define certain parameter-dependent systems that can be analysed using bifurcation theory. This method yields conclusions about the structure of periodic solutions in the original systems: Near so-called normal periodic orbits they appear in families which depend on the number of conserved quantities of the system. In Hamiltonian systems it is even possible to use the systems' symmetries to reduce the family to one branch of periodic solution that generates the whole family.
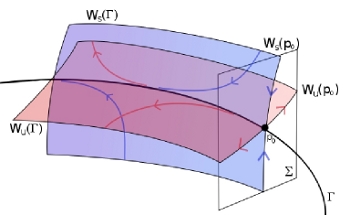
In my thesis I also studied the stable and unstable manifolds of periodic solutions. These invariant manifolds locally divide the phase space into areas with different dynamical behaviour. This is schematically shown in the picture on the right. The new aspect of my work was the derivation of a convergence estimate for their numerical approximation by forward integration of initial values in the stable and unstable subspaces of the periodic solution.
Internship project: The ISOMAP Algorithm for Nonlinear Dimensionality Reduction
Computational Biology and Biophysics Group, Jülich Supercomputing Centre
Supervisor: Dr. Thomas Neuhaus>
August - October 2007
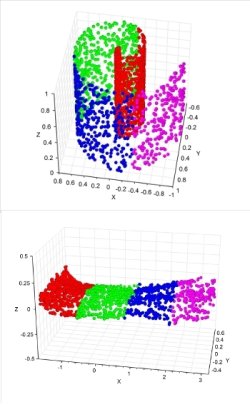
In many areas such as physics, engineering, astronomy and biology scientists have to analyse and visualise high-dimensional data sets. During my internship at the Jülich Supercomputing Centre I studied a numerical algorithm for nonlinear dimensionality reduction which was developed by Tenenbaum et al. to help understand the intrinsic degrees of freedom and the underlying geometry of such data sets.
The algorithm approximates geodesic distances between the data points by taking the shortest path on a graph where only neighboring points are connected. The points then are projected onto a lower dimensional manifold while preserving the geometric properties represented by the geodesic structure of the data set.
On the right hand side you see a set of test data in form of a “swiss roll” embedded in the three-dimensional space. Though the output data of the algorithm seems to show the intrinsic dimesion quite well, one has to be aware that the result strongly depends on the definition of “neighboring points”.