
The 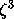 model is the
three-dimensional vector field
model is the
three-dimensional vector field
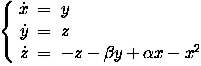
with parameters
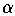 and
and
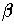 . this
system has two equilibria, one at the origin and one at B =
(
. this
system has two equilibria, one at the origin and one at B =
(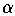 , 0, 0).
, 0, 0).
We take 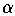 = 3.2 and
= 3.2 and
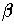 =
2. For these parameter values, the point B is unstable
due to a Hopf bifurcation at
=
2. For these parameter values, the point B is unstable
due to a Hopf bifurcation at 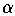 =
= 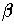 = 2. The attracting periodic orbit
that appears in this Hopf bifurcation becomes of saddle type due to a
period-doubling bifurcation. This means that one of its Floquet
multipliers moved through -1 and the unstable manifold is,
therefore, non-orientable. In fact, also the stable manifold of this
periodic orbit is topologically a Möbius strip. The animations
below show the stable and unstable manifolds.
= 2. The attracting periodic orbit
that appears in this Hopf bifurcation becomes of saddle type due to a
period-doubling bifurcation. This means that one of its Floquet
multipliers moved through -1 and the unstable manifold is,
therefore, non-orientable. In fact, also the stable manifold of this
periodic orbit is topologically a Möbius strip. The animations
below show the stable and unstable manifolds.
The two-dimensional unstable manifold of the equilibrium (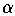 , 0, 0) accumulates
on the attracting period-doubled periodic orbit. An impression of the
structure of this manifold can be obtained by considering a
Poincaré section and rotating this section over 360
degrees.
, 0, 0) accumulates
on the attracting period-doubled periodic orbit. An impression of the
structure of this manifold can be obtained by considering a
Poincaré section and rotating this section over 360
degrees.
| Accumulation | Two stills showing the period-doubled attractor and the unstable manifold of B accumulating on it. |
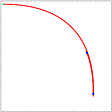
| Heteroclinic intersection |
The unstable manifold of B forms a generic heteroclinic intersection with the non-orientable stable manifold of the periodic orbit. |
 |
The animated gif shows the unstable manifold of
B = (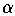 ,
0, 0) in a rotating Poincaré section. The attractor
appears as a pair of period-two points in the section. Note how the
Poincaré sections "glue" one point of the attractor to the
other after one rotation (215KB). ,
0, 0) in a rotating Poincaré section. The attractor
appears as a pair of period-two points in the section. Note how the
Poincaré sections "glue" one point of the attractor to the
other after one rotation (215KB). |