The following model is an example of a three-dimensional vector field exhibiting all types of homoclinic bifurcations. It was developed by Björn Sandstede and in a simplified form, the equations are
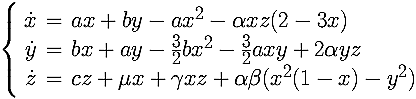
We choose fixed parameters a = 0.125, b = 0.875,
c = -2,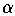 
= 1, 
= 1, 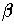and 
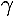= 3. The parameter 
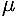is the continuation parameter.
The origin is always an equilibrium. For 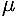< 0 a twisted saddle periodic orbit
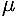exists that disappears in a twisted homoclinic bifurcation at = 0.
 |
The animated gif shows the unstable manifold rotating about the z-axis, centered at B (3.4MB). |