Growing (un)stable manifolds

of the

quasiperiodically forced Hénon map

Bernd Krauskopf & Hinke Osinga

This web page features Mpeg movies of the quasiperiodically forced Hénon map, produced with the Q2D algorithm described in ``Growing 1D and quasi 2D unstable manifolds of maps'' ( abstract), J. Comp. Phys. 146(1): 404-419, 1998.

The quasiperiodically forced Hénon map is defined as

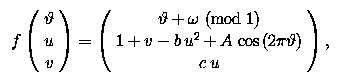
where 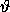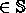¹ and u, v 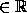. Furthermore, 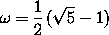is a fixed quasiperiodic rotation in 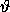, and A, b and c are parameters. For more details, we refer to the general reference.

The following movies show what happens as the parameter b changes, while A and c are fixed at A = 0.7 and c = 0.1, respectively. In all movies there is a smooth invariant circle of saddle-type, and one side of its unstable manifold is particularly interesting. This circle is shown in green, its stable manifold is blue, and its unstable manifold is red. Attractors are shown in yellow.

For b = 0.5 the unstable manifold accumulates on a smooth attracting invariant circle. The stable manifold forms the boundary of the basin of attraction (114K).
For b = 0.7 the attracting invariant circle has transformed into a strange nonchaotic attractor. The unstable manifold accumulates on this attractor (180K).
For b = 0.77 the attractor is chaotic. Note that the attractor has grown and develops peaks that are about to touch the stable manifold (209K).
For b = 0.8 the attractor has disappeared, apparently because it touched its own basin boundary. As a result, the unstable manifold is intersecting the stable manifold. Note that the dynamics flips the two sides of the stable manifold, so that the homoclinic intersections involve both sides (170K).
For b = 0.85 the homoclinic intersections are more pronounced. The unstable manifold intersects the stable manifold in a set of small circles. The top intersection gets mapped to the lowest one, on the other side of the stable manifold. The peaks developed by the unstable manifold get longer and flatter as they are closer to the invariant circle of saddle-type (185K).

Note: In the paper Globalizing two-dimensional unstable manifolds of maps, we computed heteroclinic intersections of stable and unstable manifolds (for A = 0.1, b = 0.68 and c = 0.1) with the general 2D algorithm.

Strange nonchaotic attractor: an attractor that is strange in a geometrical sense (is fractal), but does not show sensitive dependence on initial conditions (is not chaotic) because all Lyapunov exponents are negative.

General reference: O. Sosnovtseva, U. Feudel, J. Kurths, and A. Pikovsky, "Multiband strange nonchaotic attractors in quasiperiodically forced systems", Physics Letters A 218:255--267, 1996.

Creation Date: 25 June 1998

Up: VUTH eprints
Alt1: Home Page of Bernd Krauskopf
Alt2: Home Page of Hinke Osinga

	For b = 0.5 the unstable manifold accumulates on a smooth attracting invariant circle. The stable manifold forms the boundary of the basin of attraction (114K).
	For b = 0.7 the attracting invariant circle has transformed into a strange nonchaotic attractor. The unstable manifold accumulates on this attractor (180K).
	For b = 0.77 the attractor is chaotic. Note that the attractor has grown and develops peaks that are about to touch the stable manifold (209K).
	For b = 0.8 the attractor has disappeared, apparently because it touched its own basin boundary. As a result, the unstable manifold is intersecting the stable manifold. Note that the dynamics flips the two sides of the stable manifold, so that the homoclinic intersections involve both sides (170K).
	For b = 0.85 the homoclinic intersections are more pronounced. The unstable manifold intersects the stable manifold in a set of small circles. The top intersection gets mapped to the lowest one, on the other side of the stable manifold. The peaks developed by the unstable manifold get longer and flatter as they are closer to the invariant circle of saddle-type (185K).