Up:
VUTH eprints
Alt1:
Home Page of Bernd Krauskopf
Alt2:
Home Page of Hinke Osinga
This web page features Mpeg movies of the quasiperiodically forced
Hénon map, produced with the Q2D algorithm described in
``Growing 1D and quasi 2D unstable manifolds of maps''
The quasiperiodically forced Hénon map is defined as
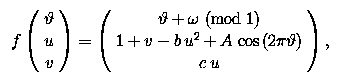
where 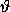
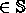 1 and u, v
1 and u, v 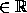 .
Furthermore,
.
Furthermore, 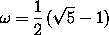 is a fixed
quasiperiodic rotation in
is a fixed
quasiperiodic rotation in 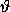 ,
and A, b and c are parameters.
For more details, we refer to the
general reference.
,
and A, b and c are parameters.
For more details, we refer to the
general reference.
The following movies show what happens as the parameter b changes, while A and c are fixed at A = 0.7 and c = 0.1, respectively. In all movies there is a smooth invariant circle of saddle-type, and one side of its unstable manifold is particularly interesting. This circle is shown in green, its stable manifold is blue, and its unstable manifold is red. Attractors are shown in yellow.

| For b = 0.5 the unstable manifold accumulates on a smooth attracting invariant circle. The stable manifold forms the boundary of the basin of attraction (114K). |

| For b = 0.7 the attracting invariant circle has transformed into a strange nonchaotic attractor. The unstable manifold accumulates on this attractor (180K). |

| For b = 0.77 the attractor is chaotic. Note that the attractor has grown and develops peaks that are about to touch the stable manifold (209K). |

| For b = 0.8 the attractor has disappeared, apparently because it touched its own basin boundary. As a result, the unstable manifold is intersecting the stable manifold. Note that the dynamics flips the two sides of the stable manifold, so that the homoclinic intersections involve both sides (170K). |

| For b = 0.85 the homoclinic intersections are more pronounced. The unstable manifold intersects the stable manifold in a set of small circles. The top intersection gets mapped to the lowest one, on the other side of the stable manifold. The peaks developed by the unstable manifold get longer and flatter as they are closer to the invariant circle of saddle-type (185K). |
Note: In the paper Globalizing two-dimensional unstable manifolds of maps, we computed heteroclinic intersections of stable and unstable manifolds (for A = 0.1, b = 0.68 and c = 0.1) with the general 2D algorithm.
General reference: O. Sosnovtseva, U. Feudel, J. Kurths, and A. Pikovsky, "Multiband strange nonchaotic attractors in quasiperiodically forced systems", Physics Letters A 218:255--267, 1996.