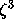 model
model 
The Lorenz system is the three-dimensional vector field
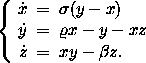
We choose the standard parameter values
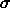 = 10,
= 10,
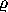 = 28, and
= 28, and
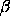 = 8/3, for
which the well-known "butterfly" attractor exists.
= 8/3, for
which the well-known "butterfly" attractor exists.
The origin is always a fixed point. For our choice of parameters, it has a two-dimensional stable and a one-dimensional unstable manifold. We show both manifolds in the pictures, but our main goal is to explore the geometry of the stable manifold and how it interacts with the attractor. The one-dimensional unstable manifold is computed with DsTool, using 50 initial points and 20,000 iterations. The two-dimensional stable manifold is computed up to arclength 100.
| Rotation Gallery | A series of pictures of the stable manifold as it is rotated about the z-axis. |
| Closeup Gallery | Several closeup views of the manifolds and the attractor. |
| Mesh Adaptation | Closeup views of the manifolds show how mesh points are automatically added or removed during the computation. |
|
| |
 |
An animated gif shows how the stable manifold grows, while focusing on how it spirals inside the attractor (2.5MB). Smaller version (872KB). |
|
| |
 |
Another animated gif shows how the stable manifold grows, while focusing on the helix that is being formed around the z-axis (1.8MB). Smaller version (638KB). |
 model
model
Multimedia supplement for "Two-dimensional global manifolds of vector
fields"
by Bernd Krauskopf and Hinke Osinga, CHAOS 9(3) (1999).
Created by Hinke Osinga
Last modified: Thu Jul 1 15:30:52 1999