
The 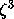 model is the three-dimensional
vector field
model is the three-dimensional
vector field
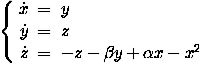
with parameters
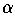 and
and
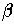 . This
system has two equilibria, one at the origin and one at B = (
. This
system has two equilibria, one at the origin and one at B = (
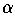 , 0,
0).
, 0,
0).
We take
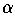 =
2.5 and
=
2.5 and
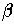 =
2. The point B is attracting for 0 <
=
2. The point B is attracting for 0 <
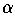 <
<
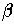 =
2 and becomes unstable via a Hopf bifurcation at
=
2 and becomes unstable via a Hopf bifurcation at
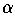 =
2. The unstable manifold of B accumulates on an
attracting periodic orbit for
=
2. The unstable manifold of B accumulates on an
attracting periodic orbit for
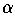 =
2.5.
=
2.5.
| Convergence process | When the manifold grows so large that it hits the limit cycle (typically only in one point at first), the convergence process starts. |
| Mesh | The bands of the manifold are two rings of points connected by triangles. The points lie on rays from the fixed point B. If necessary, more rays are added during the computation. |
| Dynamics | The algorithm grows the manifold in a way that does not reflect the dynamics on the manifold; compare the colored bands with an orbit on the manifold. |
|
| |
 |
We get an idea of the shape of the unstable manifold of B by rotating it about the x-axis. (272KB). Smaller version (133KB). |
|
| |
 |
As the unstable manifold of B grows, it hits the attracting limit cycle, after which the convergence process begins (338KB). Smaller version (173KB). |
Multimedia supplement for "Two-dimensional global manifolds of vector
fields"
by Bernd Krauskopf and Hinke Osinga, CHAOS 9(3) (1999).
Created by Hinke Osinga
Last modified: Thu Jul 1 15:30:04 1999