We found an interesting change in the scaling behavior of tongues with nonzero rotation number as they accumulate on the main tongue. We looked at tongues with rotation number 1/Fk, where Fk is the kth Fibonacci number. The scaling law differs depending on whether the main tongue has (numerically) zero or nonzero width.
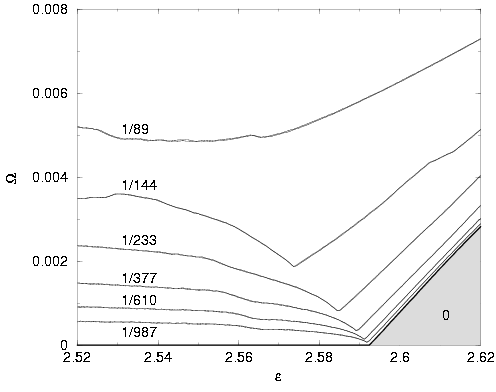
Figure 19:
Section K = 0.99 of the regions with rotation numbers
1/Fk, k being 11, ..., 16, close to the
(grey) region with zero rotation number; compare Figure 11 (left) and Figure 12.
The distance |
- 0| goes linearly with
the rotation number for parameters (
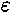, K) such that 0 = 0, but it is the square of the rotation
number otherwise.
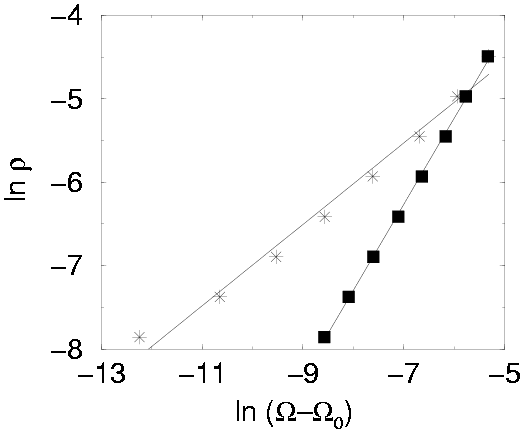
Figure 20:
The distance of the tongue with rotation number
1/Fk to the main tongue, where k ranges
from 11 to 18; compare also Figure 19. The data
can be approximated by straight lines in a ln-ln plot with slopes
1.032 +/- 0.013 for 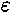= 2.55
(squares) and 0.488 +/- 0.025 for 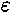= 2.61 (stars). The nonlinearity K is in both
cases equal to 0.99.
We used two different techniques to check whether we had SNA before
the nonsmooth pitchfork bifurcation or only at the moment of
bifurcation itself (the fractalization of a smooth invariant
curve). In Figure 21 we computed the phase
sensitivity for 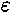-values around
the nonsmooth pitchfork bifurcation point for K = 0.9, using
a maximum of F43 iterations.
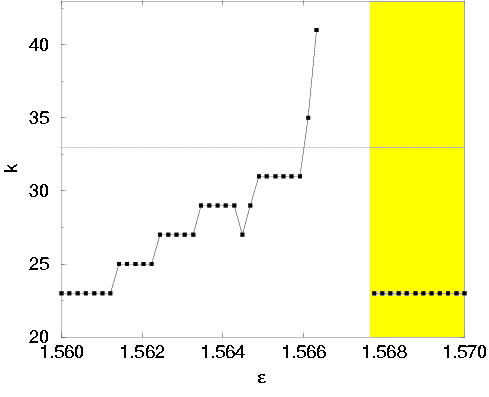
Figure 21:
Minimum number of iterations Fk for which the
phase sensitivity saturates, as a function of 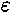, with K = 0.9 and = 0. Compare with Figure 6, where k = 33
(dashed line) is used as a threshold. In the yellow marked interval
the phase sensitivity always saturates for k = 23, indicating
two smooth attracting invariant curves. In the white marked interval
with 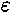smaller than
approximately 1.566 saturations occurs for k < 41,
indicating a quite wrinkled but smooth attracting invariant
curve. Using a maximum of F43 iterations, there is
no saturation for larger .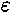
The gap before the nonsmooth pitchfork bifurcation in Figure 21 suggests that we have SNA in that region. However, if we use rational approximations and compute the maximum derivative as an approximation of the phase sensitivity, we do not get this gap; see Figure 22.
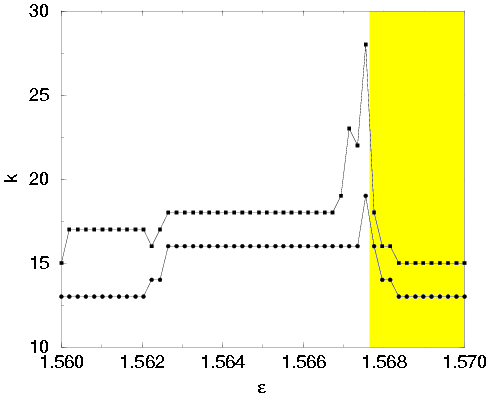
Figure 22:
Minimum order k of the rational approximation for which the
sensitive dependence on the initial phase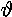 
0 vanishes (lower curve) and for which the
maximum derivative of the attracting sets in 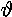0 in [0,1) saturates (upper curve), as a
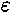function of with K =
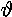0.9 and = 0; cf. Figure 21. We used 1000 different values of 0 \in [0,
1/Fk).
Created by Hinke Osinga
Last modified: Wed May 17 16:11:01 2000