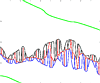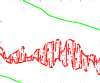
Multistability and nonsmooth bifurcations in the quasiperiodically forced circle map
	Hinke Osinga, Jan Wiersig, Paul Glendinning and Ulrike Feudel

The quasiperiodically forced circle map is a map on the torus with lift

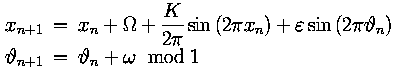
where 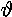_n and x_n modulo 1 give the coordinates on the torus. The parameter is the phase shift, K denotes the strength of the nonlinearity (K > 0), 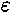is the forcing amplitude, and the forcing frequency 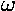is irrational.

We use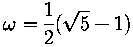

in all our computations.

We are mainly interested in the bifurcations that happen inside the tongue with zero rotation number. The boundary of this tongue is described by the function 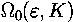the absolute value of which is shown in Figure 1.

Figure 1:	The boundary of the phase-locked region with zero rotation number; in [0, 5] runs from left to right, K in [0, 1] from back to front, and in [0, 0.16] from bottom to top. The red area corresponds to SNAs.

Inside the main tongue there are regions where more than one attractor exist simultaneously. We study these regions by looking at sections in the parameter space: in one section we keep K = 0.8 fixed, in the other we take = 0. For large nonlinearity K the bifurcations change from smooth to nonsmooth. We discuss both the saddle-node and pitchfork bifurcations and study codimension-2 points as well.

The internal structure for K = 0.8	The bifurcation structure in the (, K)-plane	The nonsmooth pitchfork bifurcation	The nonsmooth saddle-node bifurcation	A nonsmooth bifurcation point of codimension two