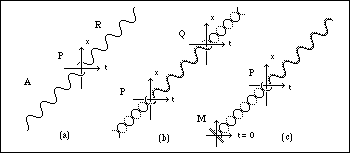
Fig 4: (a) Advanced and retarded waves, (b) Emitter-absorber transaction, (c) Reflecting boundary condition at origin of the universe results in retarded radiation.
(5) King C.C., (1989), Dual-Time Supercausality Physics Essays 2/2 128-151.
This article explores models of causality of the physical universe which extend beyond the usual quantum and classical descriptions. To facilitate discussion of this topic, a brief review of relevant areas of modern physics is included.
Although mathematical logic is not directed in time, the causal description of the physical universe is classically performed in terms of temporal determinism, an initial-value problem in which subsequent states are determined through the action of differential equations, thus avoiding the paradox of effects preceding their causes. Quantum mechanics has reduced this description to the status of a stochastic-causal theory, in which individual future states of a system are not predictable because the probability interpretation of the wave function prevents a complete knowledge of a single reduction of the wave packet.

Fig 4: (a) Advanced and retarded waves, (b) Emitter-absorber transaction,
(c) Reflecting boundary condition at origin of the universe results in retarded
radiation.
The transactional interpretation of quantum mechanics provides a basis for examining the workings of stochastic causality in terms of time-symmetric advanced and retarded waves. Cosmic symmetry-breaking provides a contrasting description in which time-directed phenomena derive their explanation.
Dual-time supercausality replaces the stochastic model with one in which two complementary causal processes, symmetric-time and directed-time are operating. The mode of interaction of these avoids temporal paradox in the time-directed description, and also explains why quantum mechanics provides an incomplete stochastic model.
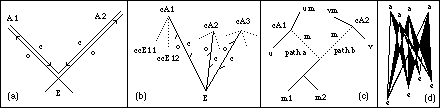
Fig 13: (a) Retrospective light-cones of the absorbers join at the emission
vertex in the pair-splitting experiment. (b) Confirming waves of contingent
absorbers are resolved at the emission vertex in a one-particle transaction.
(c) A polymerization reaction involving emission of contingent absorbers
of a molecular intermediate m. (d) Enfolding of contingent offers and confirmations
into a spliced space-time interaction. An important role for supercausal
processes in the structural evolution of the universe is proposed, including
the emergence of biosystems, biological evolution, and consciousness.
Excerpt 1: In the transactional interpretation, we have the collapse being determined across space-time by the action of the boundary conditions on the confirmation waves arising from the contingent absorbers. The transactional interpretation provides for a non-linear wave transient acting at the emission and absorption vertices determining the collapse dynamics of the event, in a form which I will call transactional transcausality. In figure 13, (a) shows the transaction for the pair-splitting experiment. There is no need for a superluminal interaction to connect the absorption events A1 and A2 because their retrospective light cones intersect at the emission vertex in space-time. It doesn't matter which one if A1 and A2 are first or which is deemed to collapse the paired wave function, because the transaction is established across the space-time of the entire light cone from E.
If we apply the same treatment to the resolution of the collapse dynamic of all contingent confirmation waves by all contingent absorbers, we have a similar effect. Regardless of the time or position of a given contingent absorption event, the contingent confirmation waves all arrive simultaneously at the emission vertex, and in the case of a single particle event are resolved by the boundary conditions into a single transaction. One way of describing this resolution is through a non-linear transient in the total confirmation wave. Because this is established both prospectively and retrospectively it would result in a supercausal description of the collapse dynamic. Such a transient must be consistent with the probability norm, rather than a simple bifurcation favoring the maximal contributor.
Transaction can also explain the origin ofthe arrow of time as a reflecting boundary condiditon at the origin of the universe giving rise to a real positive-energy universe.
Other views of the arrow of time Paul Davies
Excerpt 2: (1) Internal symmetries and Pseudo-stochastic theories. It is possible to mount an empirical approach to discovering relationships between collapse events. We will merely examine pointers to how dual causalities might be modelled in a manner consistent with the probability interpretation. We have seen that the data from each end of a pair-splitting experiment behaves individually as random data which conforms to the probability interpretation. However, when the data is compared at both ends, the correlation between the individual sets of data becomes apparent. The data at each end appears random because it is encrypted through the wave function of the pair. We can extend this reasoning to look for internal symmetries in the collapse process which might connect the collapse of many wave functions across a space-time interval through correlations between their individual statistics. Internal symmetries might for example relate indistinguishable particles, all wave functions in a given class, ( e.g. all N7 nitrogens of the adenine molecule ), or in a more restrictive scheme, all equivalent interactions in which a given measurement relationship occurs ( such as all interactions between a given enzyme and its substrate ). Alternatively they may relate contingent sets in a transaction. In the case of transactional transcausality the internal symmetry is the space-time splicing of super-contingent transactions. I.e. all the contingent emissions and absorptions which are indirectly connected to y as described in fig 13(d). The obvious constraint that must be placed on such a symmetry is that it should approximate the probability interpretation to first order. A deterministic function is termed pseudo-random, if a sequence of values satisfy suitable non-periodicity, chi-squared or other test criteria generally satisfied by a random distribution. A complex dual process may be consistent with quantum-mechanics simply by virtue of its pseudo-randomness, despite having a unique selection property over space-time. We will call such a theory pseudo-stochastic.
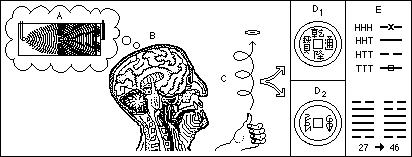
Fig 16: Reversed Cat paradox experiment. A quantum wave-particle reduction, A triggers a structurally unstable brain state B. This in turn triggers a structurally unstable physical process C, giving rise to two possible outcomes, D1 and D2. The system may be refined by using sequential reductions to generate an interpretation E.
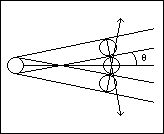
Excerpt 3: If we return for a minute to the ideal gas, we can estimate the contribution made by spreading of the wavefront to the statistical mechanics of particle motion. In particular one can define the indeterminacy radius of a particle as the distance travelled before the diffraction of the particle is twice the particle diameter, as in fig 14(b), resulting in complete uncertainty of the direction in the elastic collision. ... Since the wavelength varies inversely with the square root of the molecular weight of a molecule at a given temperature, we can make a realistic estimate of the indeterminacy radius of an amino acid in aqueous solution as follows. The average molecular weight is approximately 120. The wavelength is thus .18/120 = .017 If we take the length of an amino acid as .36 nm and use the formula sin(q) = +/- l/w to estimate the angle q of the above figure using a .15 nm diameter of a water molecule as w, we find sin(q) = .017/.15 or q = 6.5 degrees. Thus in .36 nm the uncertainty of position would be .0408 approximately the Bohr radius. The uncertainty will thus become complete after a few kinetic encounters.