Back to Preprints

(7) King C.C., (1991), Fractal and Chaotic Dynamics in Nervous Systems. Progress in Neurobiology 36 279-308.

The full paper can be read or downloaded (in Acrobat Reader (pdf)) format.

This paper presents a review of fractal and chaotic dynamics in nervous systems and the brain, exploring mathematical chaos and its relation to processes, from the neurosystems level down to the molecular level of the ion channel. It includes a discussion of parallel distributed processing models and their relation to chaos and overviews reasons why chaotic and fractal dynamics may be of functional utility in central nervous cognitive processes. Recent models of chaotic pattern discrimination and the chaotic electroencephalogram are considered. A novel hypothesis is proposed concerning chaotic dynamics and the interface with the quantum domain.

This review surveys fractal and chaotic processes in brain dynamics and provides workers in experimental fields with a compact source of material in mathematical chaotic dynamics as a reference. An attempt has been made to make the mathematical aspects of the paper remain approachable to a variety of readers. Full background references are given to enable the reader to gain further in-depth treatment, and to explore more fully the variety of specialist topics leading out from the discussion.

Section 1 provides a compact mathematical introduction to fractal and chaotic dynamics. Most of the systems discussed here have specific application to experimental results in later sections. Sections 2 and 3 complement this with source material on mathematical modelling of neural nets and on biological neurons. In section 4 chaos at the cellular level is discussed, including models of the excitable membrane and ion channel. In section 5 chaotic neurosystems models and experimental results are considered including the Freeman-Skarda model and studies of the EEG. Section 6 touches on issues connecting quantum chaos, causality and the mind.

Fig 4 : The logistic map : (a) The forms of the attractor, Liapunov exponent and Mandelbrot set, for 2.8 < r < 4 showing the development of multiple period doublings, chaotic regions and periodic windows. The attractor initially is a single curve (point attractor) but then repeatedly subdivides (pitchfork bifurcations) finally entering chaos (stippled band). Subsequently there are windows of period 3, 5 etc. with abrupt transitions from and to chaos caused by intermittency and crises. The Liapunov exponent l < 0 until chaos sets in. During chaos it remains positive. The Mandelbrot set illustrates the fractal nature of the periodic and chaotic regimes when x , r are extended to the complex number plane. Complex number representation aids visualizing such fractal structures. (b) A series of 2-D iterations of Gr(xn) including periods 1, 2 and 8 chaos, intermittency, and period 3. In (i) the two-step iteration process is illustrated alternately evaluating y = r x (1 - x) (vertical) and x = y (horizontal). As r crosses the value 1 a saddle-node bifurcation occurs resulting in the attractor moving from zero and leaving a repellor there (r = 2). In (ii) and (iii) period 2 and 8 attractors have formed. In (iv) the iteration has become chaotic. In (v) the chaos is intermittently entering a period 3 regime, which has become stable in (vi). (c) The Cantor set of the horseshoe for r = 4.5. The attractor has now broken up resulting in most points iterating to minus infinity, leaving only a Julia set of exceptional points. (d) The pitchfork bifurcation illustrated. The double iterate Gr2(xn) twists to cross y = x an extra time, resulting in doubling of the attractor into a period 2 set. (e) The tangent bifurcation illustrated using the triple iterate Gr3(xn). The lifting of the central tangent above y = x removes the stability of period 3 causing slippage and intermittent chaos.

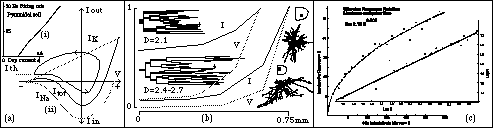Fig 11 : (ai) Piecewise-linear response of a Pyramidal cell to depolarizing current. (aii) S-curve of current flow with voltage results from the sum of Na+ and K+ currents. The resulting action limit cycle has an abrupt threshold I th at which the cycle triggers. (b) Fractal structures of superior colliculus dendrites and the exponential decline of I and V with distance. Note the improved current characteristics of the tree with a lower fractal dimension. (c) Non-linear (approximately inverse quadratic) response of touch receptors, indicating a general non-linear response to membrane deformations.

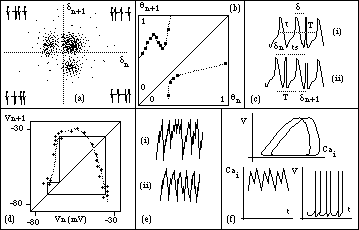
Fig 14 : (a) Clumping in successive periods in ECG is indicative of chaos rather than noise, (Babloyantz 1989). The figure plots successive delays, demonstrating a non-random spread. (b) The form of g(q) in chicken heart cells, from a qn- qn+1 plot. This closely approximates the form of the circle map function fig 5(e) justifying the use of the circle map in the model. (c) Periods in chicken heart aggregates used to develop the model in detail. (d) Period 3 attractor in Nitella, interpolation of the transfer function by taking repeated iterates and plotting Vn+1 against Vn to form the analogue of the figures in fig 4(b) for this map. (e) Forms of chaotic waveforms in the Chay-Rinzel model (bursting) in Nitella. (f) period doubling in Chay-Rinzel model (beating) shown by plots of V, Ca and t together.

The aim of the review is to make it possible for a reader to gain a comprehensive overview of chaos as it applies to neural processes, to compare chaotic models with their alternatives and to assess the scope of chaotic and fractal processes in the conceptualization of the physical basis of brain function.

To return to publications (click publications)