Boundary crisis in
|
 |
Boundary crisis in
|
 |
This is a joint project with Ulrike Feudel, University of Potsdam (Germany). We study boundary crisis in quasiperiodically forced systems using the Hénon map as a characteristic example. The quasiperiodically forced Hénon map is defined as
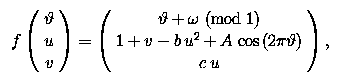
with 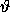
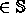 1 and u, v
1 and u, v
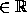 . We consider the two-parameter family
of maps in (A, b)-space where
. We consider the two-parameter family
of maps in (A, b)-space where
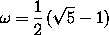 is a fixed quasiperiodic
rotation in
is a fixed quasiperiodic
rotation in 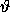 , and c = 0.1.
, and c = 0.1.
A boundary crisis is the sudden disappearance of a chaotic attractor as it hits an unstable (periodic) set on its basin boundary. For example, if we take A = 0.2 the attractor becomes chaotic approximately for b = 0.896 and runs into an invariant circle of saddle type approximately for b = 1.334.