Multimedia supplement for the paper
Two-dimensional invariant manifolds in four-dimensional dynamical systems
by Hinke Osinga

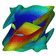
This paper explores the visualization of two-dimensional stable and unstable manifolds of the origin (a saddle point) in a four-dimensional Hamiltonian system arising from control theory. The manifolds are computed using an algorithm that finds sets of points that lie at the same geodesic distance from the origin. By coloring the manifolds according to this geodesic distance, one can gain insight into the geometry of the manifolds and how they sit in four-dimensional space. This is compared with the more conventional method of coloring the fourth coordinate. We also take advantage of the symmetries present in the system, which allow us to visualize the manifolds from different viewpoints at the same time.

	Rotation in (x1, x2, p1)-space
	Rotation in (x2, p1, p2)-space